S Ut 1 2at 2 Solve For T
aseshop
Sep 13, 2025 · 6 min read
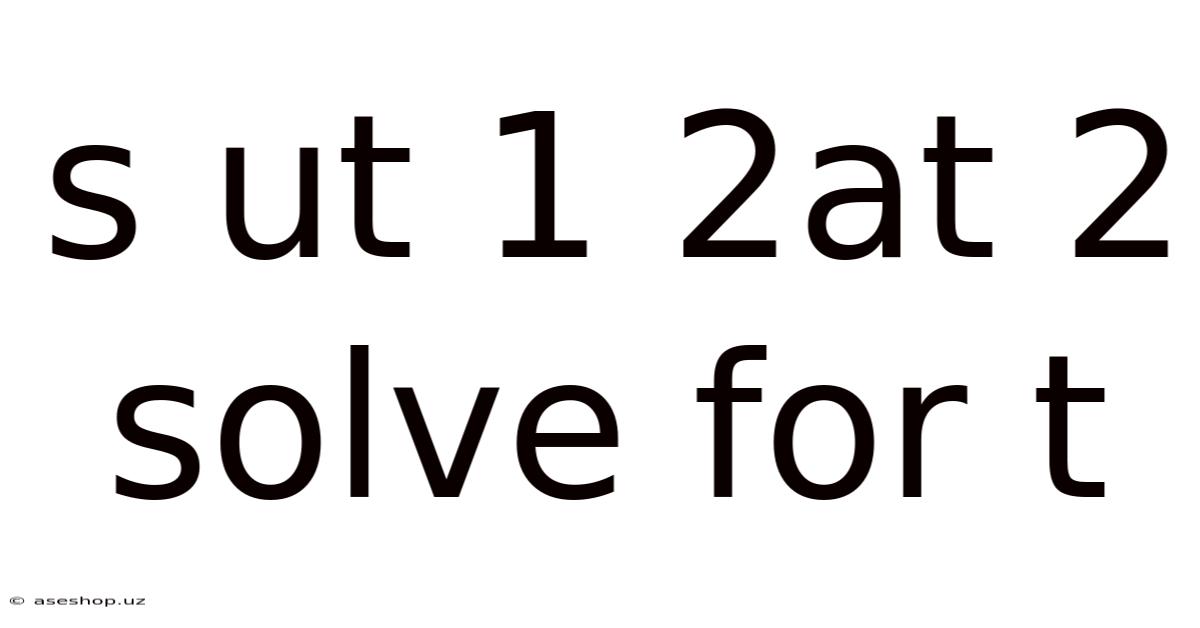
Table of Contents
Solving for 't': A Comprehensive Guide to Understanding and Applying the Equation s = ut + 1/2at²
This article provides a comprehensive guide to understanding and solving the kinematic equation s = ut + (1/2)at², a fundamental formula in physics used to describe the motion of objects under constant acceleration. We will delve into its derivation, explore various scenarios for its application, and address common challenges faced when solving for 't'. This equation, which relates displacement ('s'), initial velocity ('u'), acceleration ('a'), and time ('t'), is crucial for understanding projectile motion, free fall, and many other aspects of classical mechanics.
Understanding the Variables
Before diving into solving for 't', let's clearly define each variable in the equation:
-
s: This represents the displacement or the change in position of the object. It's a vector quantity, meaning it has both magnitude and direction. A positive value indicates displacement in the positive direction, while a negative value indicates displacement in the negative direction. Units are typically meters (m).
-
u: This represents the initial velocity of the object, the velocity at the beginning of the time interval considered. It's also a vector quantity with units of meters per second (m/s).
-
a: This represents the constant acceleration of the object. Acceleration is the rate of change of velocity. It's a vector quantity with units of meters per second squared (m/s²). Note that the equation only applies when acceleration is constant.
-
t: This represents the time elapsed during the motion. It's a scalar quantity (only magnitude) with units of seconds (s).
Deriving the Equation: A Visual Approach
The equation s = ut + (1/2)at² is derived from the basic principles of motion under constant acceleration. We can visualize this using a velocity-time graph.
Imagine an object moving with constant acceleration 'a'. Its initial velocity is 'u'. The area under the velocity-time graph represents the displacement 's'. This area can be divided into two parts:
-
A rectangle: With width 't' and height 'u', representing the displacement covered at constant initial velocity. The area of this rectangle is ut.
-
A triangle: With width 't' and height 'at' (since acceleration is the change in velocity over time, the change in velocity is 'at'). The area of this triangle represents the additional displacement due to acceleration. The area of a triangle is (1/2) * base * height, giving us (1/2)at².
Adding the areas of the rectangle and triangle gives us the total displacement: s = ut + (1/2)at².
Solving for 't': The Quadratic Formula
The equation s = ut + (1/2)at² is a quadratic equation in terms of 't'. This means it contains a t² term. To solve for 't', we need to rearrange the equation into the standard quadratic form:
at² + 2ut + (-2s) = 0
This equation is now in the form of ax² + bx + c = 0, where:
- a = a (acceleration)
- b = 2u (twice the initial velocity)
- c = -2s (negative twice the displacement)
We can now use the quadratic formula to solve for 't':
t = [-b ± √(b² - 4ac)] / 2a
Substituting the values of a, b, and c from our equation, we get:
t = [-2u ± √((2u)² - 4a(-2s))] / 2a
This formula will give you two solutions for 't'. The physical significance of these solutions depends on the context of the problem. One solution might represent the time it takes for the object to reach a particular displacement, while the other might be irrelevant (e.g., a negative time value). Always consider the physical context to determine which solution is meaningful.
Practical Examples and Applications
Let's illustrate the solution process with some examples:
Example 1: A ball thrown upwards
A ball is thrown vertically upwards with an initial velocity of 20 m/s. It experiences a constant downward acceleration due to gravity (approximately 9.8 m/s²). How long does it take for the ball to reach a height of 15 meters?
Here's how to solve it:
- s = 15 m (displacement)
- u = 20 m/s (initial velocity)
- a = -9.8 m/s² (acceleration due to gravity; negative because it's acting downwards)
Substitute these values into the quadratic formula:
t = [-2(20) ± √((2(20))² - 4(-9.8)(-2(15)))] / 2(-9.8)
Solving this equation will give you two values for 't'. One will be a positive value representing the time it takes to reach 15 meters on the way up, and the other will be a positive value representing the time it takes to reach 15 meters on the way down.
Example 2: A car accelerating from rest
A car accelerates uniformly from rest (u = 0 m/s) at 2 m/s² for a certain time, covering a distance of 50 meters. How long did it take to cover that distance?
- s = 50 m
- u = 0 m/s
- a = 2 m/s²
Substituting these values into the equation s = ut + (1/2)at², we get:
50 = 0*t + (1/2)(2)t²
Simplifying this equation yields:
50 = t²
Therefore, t = √50 ≈ 7.07 seconds. In this case, only one positive solution is physically meaningful.
Special Cases and Simplifications
There are special cases where the quadratic formula can be avoided:
-
When the initial velocity (u) is zero: The equation simplifies to s = (1/2)at², making the calculation much simpler. Simply solve for t² and take the square root.
-
When the acceleration (a) is zero: The equation simplifies to s = ut, implying constant velocity. Solving for 't' is straightforward: t = s/u.
Frequently Asked Questions (FAQs)
Q1: What if I get a negative value for 't'?
A negative value for 't' usually indicates a time before the motion started, which is not physically relevant. Consider only the positive solution(s) in most scenarios.
Q2: What if the discriminant (b² - 4ac) is negative?
A negative discriminant means there are no real solutions for 't'. This might indicate an impossible situation given the parameters of the problem. Double-check your values and the physical context.
Q3: Can this equation be used for non-constant acceleration?
No, this equation only applies to situations with constant acceleration. For non-constant acceleration, more advanced calculus techniques are required (integration).
Q4: How do I choose the correct solution when I get two positive values for 't'?
Carefully examine the physical context of the problem. One solution usually represents a specific point in the motion (e.g., reaching a certain height on the way up versus the way down), while the other might be extraneous.
Conclusion
Solving for 't' in the kinematic equation s = ut + (1/2)at² is a crucial skill in physics. Understanding the underlying principles, applying the quadratic formula correctly, and interpreting the results within the context of the problem are essential for mastering this fundamental concept. By practicing with various examples and considering the special cases, you'll build confidence and a strong understanding of motion under constant acceleration. Remember to always check the physical plausibility of your answer; a negative time or an unrealistic displacement should prompt you to review your calculations and assumptions. This equation provides a powerful tool for analyzing and predicting the motion of objects in a vast array of physical situations.
Latest Posts
Latest Posts
-
What Do Blue Road Signs Indicate
Sep 13, 2025
-
How Long Does A Red Blood Cell Last
Sep 13, 2025
-
What Does The Word Homeostasis Mean
Sep 13, 2025
-
Renaissance Thinker One Associated With Calvin
Sep 13, 2025
-
Summary Of Act 1 Scene 5 Macbeth
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about S Ut 1 2at 2 Solve For T . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.