Force Equal To Mass Times Acceleration
aseshop
Sep 07, 2025 · 7 min read
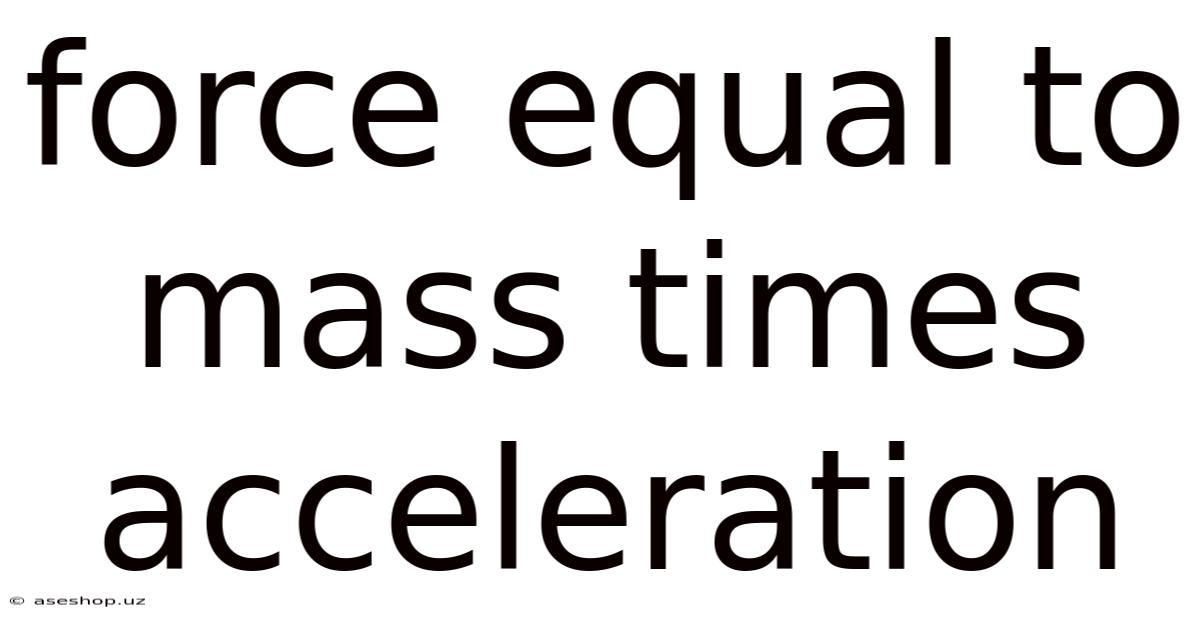
Table of Contents
Understanding Force: The Foundation of Newtonian Mechanics – Force Equals Mass Times Acceleration
Newton's second law of motion, often summarized as F = ma, is a cornerstone of classical mechanics. This deceptively simple equation, stating that force (F) is equal to mass (m) times acceleration (a), unlocks a deep understanding of how objects move and interact within the physical world. It's not just a formula to memorize; it's a powerful tool for analyzing everything from the trajectory of a baseball to the motion of planets. This article will delve into the intricacies of this fundamental law, exploring its meaning, applications, and implications.
What Does F=ma Really Mean?
At its core, F=ma describes the relationship between three fundamental physical quantities:
-
Force (F): A force is any interaction that, when unopposed, will change the motion of an object. This could be a push, a pull, friction, gravity, or any other interaction that causes an object to accelerate. Force is a vector quantity, meaning it has both magnitude (strength) and direction. It's typically measured in Newtons (N).
-
Mass (m): Mass is a measure of an object's inertia – its resistance to changes in motion. A more massive object requires a greater force to achieve the same acceleration as a less massive object. Mass is a scalar quantity (it only has magnitude) and is typically measured in kilograms (kg).
-
Acceleration (a): Acceleration is the rate at which an object's velocity changes over time. It's also a vector quantity, meaning it has both magnitude and direction. A positive acceleration indicates an increase in speed, while a negative acceleration (deceleration) indicates a decrease in speed. Acceleration is measured in meters per second squared (m/s²).
Therefore, F=ma tells us that the greater the force applied to an object, the greater its acceleration will be. Conversely, the greater the mass of an object, the smaller its acceleration will be for a given force.
Understanding the Vector Nature of Force and Acceleration
It's crucial to remember that force and acceleration are vector quantities. This means that they possess both magnitude and direction. If you push a box across the floor to the right with a force of 10 N, the acceleration of the box will also be to the right. If you then apply a force of 5 N to the left, the net force will be 5 N to the right, resulting in a reduced acceleration to the right.
This vector nature allows us to analyze complex scenarios involving multiple forces acting on an object. Using vector addition, we can determine the net force and thus the resulting acceleration. For example, consider a car accelerating uphill. The engine provides a forward force, while gravity exerts a downward force, and friction opposes the motion. The net force is the vector sum of these forces, and this net force determines the car's acceleration.
Applications of F=ma: From Everyday Life to Rocket Science
The equation F=ma is not just a theoretical concept; it's a practical tool with widespread applications:
-
Everyday situations: Consider pushing a shopping cart. The harder you push (greater force), the faster it accelerates. If you try to push a heavier cart (greater mass), it will accelerate more slowly for the same amount of force.
-
Sports: Understanding F=ma is vital in sports. The force exerted by a batter on a baseball determines its acceleration, influencing its trajectory. The force a sprinter exerts on the ground determines their acceleration during a race.
-
Engineering: Engineers use F=ma to design structures, vehicles, and machines. They need to calculate the forces required to move or support objects of different masses and predict their acceleration under different conditions. Bridge design, for instance, requires precise calculations to ensure the bridge can withstand the forces exerted upon it.
-
Rocket science: Rocket propulsion relies heavily on Newton's second law. The force generated by the rocket engines determines the rocket's acceleration, which is crucial for overcoming Earth's gravity and achieving escape velocity. The mass of the rocket, including its fuel, significantly impacts its acceleration.
-
Automotive engineering: Understanding the relationship between force, mass, and acceleration is essential for designing safe and efficient vehicles. Braking systems are designed to generate a specific deceleration (negative acceleration) based on the mass of the vehicle.
Delving Deeper: Net Force and Multiple Forces
When multiple forces act on an object, the resulting acceleration is determined by the net force. The net force is the vector sum of all individual forces acting on the object. This is often represented as:
ΣF = ma
where ΣF represents the sum of all forces. If the net force is zero, the object will either remain at rest or continue moving at a constant velocity (Newton's first law). If the net force is non-zero, the object will accelerate in the direction of the net force.
Consider a block on a frictionless surface being pulled by two forces: one of 10 N to the right and another of 5 N to the left. The net force is 10 N - 5 N = 5 N to the right. The block will accelerate to the right with an acceleration proportional to this net force and inversely proportional to its mass.
The Role of Friction in Real-World Scenarios
In many real-world situations, friction plays a significant role in determining an object's motion. Friction is a force that opposes motion between two surfaces in contact. It always acts in the direction opposite to the motion or intended motion of the object. The magnitude of frictional force depends on the nature of the surfaces and the force pressing them together (normal force).
When we consider friction, the equation becomes more complex. The net force is now the difference between the applied force and the frictional force. If the applied force is less than the frictional force, the object will not move. If the applied force is greater than the frictional force, the object will accelerate, but the acceleration will be less than it would be without friction.
Beyond F=ma: Limitations and Extensions
While F=ma is a powerful tool, it has limitations. It's most accurate for objects moving at speeds significantly less than the speed of light. At very high speeds, relativistic effects become significant, and Einstein's theory of special relativity must be considered. The equation also doesn't account for the effects of quantum mechanics, which govern the behavior of matter at the atomic and subatomic level.
Despite these limitations, F=ma remains a cornerstone of classical mechanics and provides an accurate description of motion for a vast range of scenarios. More advanced concepts, such as rotational motion and momentum, build upon this fundamental principle.
Frequently Asked Questions (FAQs)
Q: What are the units for force, mass, and acceleration in the F=ma equation?
A: The standard units are:
- Force (F): Newtons (N)
- Mass (m): Kilograms (kg)
- Acceleration (a): Meters per second squared (m/s²)
Q: How do I calculate force if I know mass and acceleration?
A: Simply multiply the mass by the acceleration: F = m * a
Q: How do I calculate acceleration if I know force and mass?
A: Divide the force by the mass: a = F / m
Q: What happens if the net force is zero?
A: If the net force acting on an object is zero, the object will either remain at rest or continue moving at a constant velocity in a straight line (Newton's First Law of Motion).
Q: How does friction affect the F=ma equation?
A: Friction opposes motion and must be considered as a force acting in the opposite direction of the applied force. The net force is the difference between the applied force and the frictional force.
Q: Is F=ma applicable to all situations?
A: While highly useful, F=ma is not universally applicable. It is primarily valid for classical mechanics and objects at relatively low speeds. At speeds approaching the speed of light, relativistic effects become significant.
Conclusion: The Enduring Power of F=ma
Newton's second law of motion, F=ma, is a fundamental principle in physics that governs the motion of objects. Its simplicity belies its power, allowing us to analyze a wide range of phenomena from everyday occurrences to complex engineering challenges. Understanding this equation is essential for grasping the basic principles of classical mechanics and provides a foundation for more advanced topics in physics and engineering. While it has its limitations, F=ma remains an indispensable tool for understanding the world around us and shaping technological advancements. Its enduring legacy underscores its crucial role in our understanding of motion and forces in the universe.
Latest Posts
Latest Posts
-
What Is The Job Of The Root Hair Cell
Sep 07, 2025
-
An Inspector Calls What Is It About
Sep 07, 2025
-
What Is The Normal Urine Output Per Hour
Sep 07, 2025
-
Hong Kong Fir Shipping V Kawasaki Kisen Kaisha
Sep 07, 2025
-
Use The Word Propaganda In A Sentence
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Force Equal To Mass Times Acceleration . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.