Expand And Simplify X 6 X 2
aseshop
Sep 25, 2025 · 6 min read
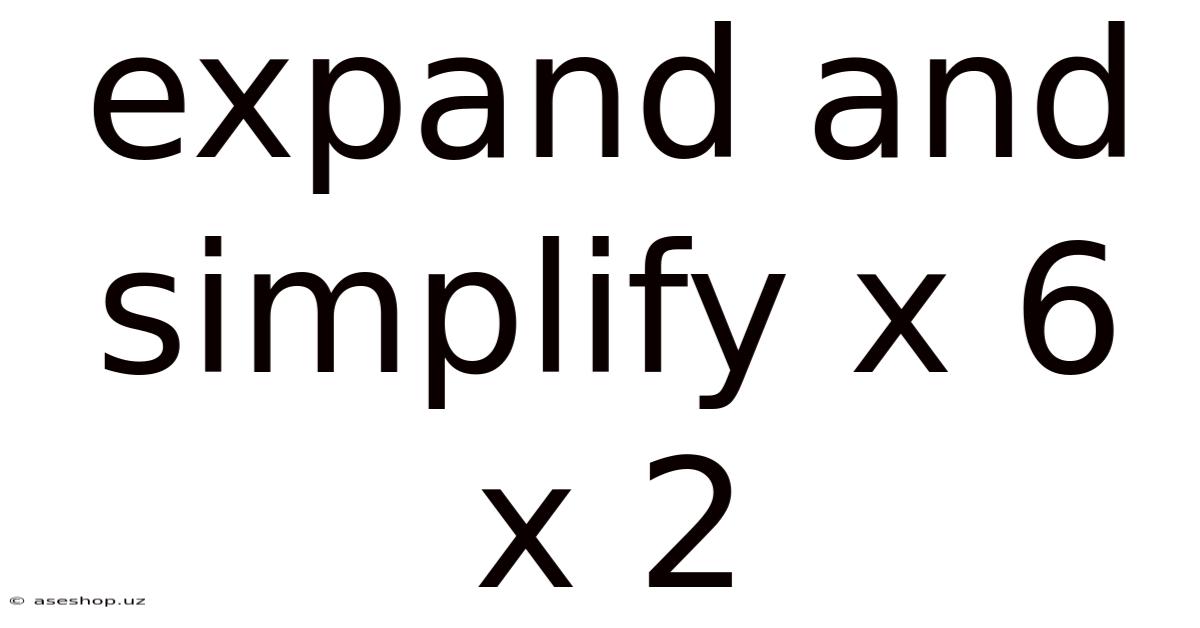
Table of Contents
Expanding and Simplifying Expressions: A Deep Dive into 6 x 2 and Beyond
This article explores the seemingly simple mathematical expression "6 x 2" and expands upon it to illustrate fundamental concepts in arithmetic, algebra, and even slightly more advanced mathematical ideas. We'll demystify the process of expanding and simplifying expressions, providing a thorough understanding suitable for learners of all levels, from elementary school students to those refreshing their mathematical foundations. Understanding how to manipulate these expressions is crucial for success in various fields, including science, engineering, and finance.
What Does 6 x 2 Mean? A Foundational Understanding
At its core, "6 x 2" represents multiplication. Multiplication is a shorthand way of representing repeated addition. In this case, it means adding the number 6 to itself two times: 6 + 6 = 12. Therefore, 6 x 2 = 12. This simple equation lays the groundwork for understanding more complex algebraic manipulations.
Expanding the Expression: Breaking it Down
While 6 x 2 is already in its simplest form, we can expand it to better illustrate the principles of multiplication. Let's consider different ways to expand this seemingly straightforward equation:
-
Repeated Addition: As mentioned earlier, 6 x 2 is equivalent to 6 + 6. This visually demonstrates the concept of repeated addition underlying multiplication.
-
Distributive Property: The distributive property of multiplication over addition is a cornerstone of algebra. While not directly applicable to 6 x 2 in its simplest form, we can create a scenario where it becomes relevant. Let's say we have (6 x 2) + (6 x 3). We can use the distributive property to expand this as follows: 6 x (2 + 3) = 6 x 5 = 30. This demonstrates how the distributive property allows us to simplify expressions involving both multiplication and addition.
-
Area Model: Visual representations are incredibly useful in understanding mathematical concepts. Imagine a rectangle with a length of 6 units and a width of 2 units. The area of this rectangle is calculated by multiplying length and width, i.e., 6 x 2 = 12 square units. This visual representation helps solidify the meaning of multiplication.
-
Prime Factorization: Every whole number greater than 1 can be expressed as a product of prime numbers (numbers divisible only by 1 and themselves). 6 can be factored into 2 x 3. Therefore, 6 x 2 can be expanded as (2 x 3) x 2. This might seem trivial in this case, but it becomes critical when dealing with more complex expressions involving larger numbers.
Simplifying Expressions: Combining Like Terms
While 6 x 2 is already in its simplest form, let's explore how to simplify more complex expressions that might involve multiplication and addition or subtraction. For instance, consider the expression 3x + 6x - 2x. Here, we have 'like terms' – terms that share the same variable (x) and exponent (implicitly 1). We can simplify this by combining these like terms: 3x + 6x - 2x = 7x.
Similarly, consider the expression: (2 x 5) + (4 x 5). This can be simplified by using the distributive property in reverse: 5 x (2 + 4) = 5 x 6 = 30. Understanding this simplification process is fundamental in algebra and beyond.
Expanding and Simplifying Algebraic Expressions
Let's move beyond simple arithmetic and delve into algebraic expressions. Consider the expression 2(x + 3). To expand this, we apply the distributive property: 2(x + 3) = 2x + 6. This demonstrates how we can distribute the multiplication over the addition within the parentheses.
Now, let's consider a more complex expression: 3x(2x + 5). We expand this using the distributive property again: 3x(2x + 5) = (3x * 2x) + (3x * 5) = 6x² + 15x. Notice that multiplying x by x results in x², highlighting the rules of exponent multiplication (x¹ * x¹ = x²).
Simplifying algebraic expressions often involves combining like terms after expansion. For example, consider the expression: 4x² + 2x + 3x² - x. Combining like terms, we get 7x² + x.
Applications in Real-World Scenarios
Understanding expansion and simplification of expressions isn't just confined to the classroom. It has numerous real-world applications:
-
Finance: Calculating interest, compound interest, and loan repayments all involve manipulating expressions that require both expansion and simplification.
-
Physics and Engineering: Many physical laws and formulas are expressed algebraically. Expanding and simplifying expressions are essential for solving problems in areas like mechanics, electricity, and thermodynamics.
-
Computer Programming: Writing efficient code often involves simplifying complex expressions to optimize performance and reduce redundancy.
-
Data Analysis: Data analysis frequently employs statistical calculations that rely on manipulating expressions to gain insights from data sets.
Beyond the Basics: More Advanced Concepts
While we’ve focused primarily on the basics, the principles of expansion and simplification extend to more complex mathematical areas:
-
Polynomial Expansion: Expanding expressions involving multiple variables and higher powers (e.g., (x + y)² or (2x² + 3x – 1)(x + 2)) often requires the use of techniques like FOIL (First, Outer, Inner, Last) or binomial theorem.
-
Factoring: The inverse of expansion is factoring, where we rewrite an expression as a product of simpler expressions. Factoring is critical in solving equations and simplifying fractions.
-
Calculus: Derivatives and integrals, the fundamental concepts of calculus, involve manipulating expressions through differentiation and integration techniques. A strong understanding of expanding and simplifying expressions is essential for success in calculus.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between expanding and simplifying?
-
A: Expanding means rewriting an expression to eliminate parentheses or brackets, often using the distributive property. Simplifying involves reducing an expression to its most concise form by combining like terms or applying other algebraic rules.
-
Q: Why is the order of operations (PEMDAS/BODMAS) important?
-
A: PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) dictates the order in which mathematical operations should be performed. Following this order ensures consistent and accurate results when evaluating expressions.
-
Q: What are like terms?
-
A: Like terms are terms in an algebraic expression that have the same variable(s) raised to the same power(s). For example, 3x and 5x are like terms, but 3x and 3x² are not.
-
Q: How can I practice expanding and simplifying expressions?
-
A: Practice is key! Work through numerous examples, starting with simpler expressions and gradually increasing the complexity. Online resources, textbooks, and practice workbooks offer ample opportunities for practice.
Conclusion
The seemingly simple expression "6 x 2" serves as a springboard to understanding the fundamental concepts of expanding and simplifying mathematical expressions. From basic arithmetic to advanced algebra and calculus, the ability to manipulate these expressions is a crucial skill in various fields. By mastering these techniques, you'll build a solid foundation for tackling more challenging mathematical problems and unlock a deeper appreciation for the elegance and power of mathematics. Remember, consistent practice and a clear understanding of the underlying principles are the keys to success. Don’t be afraid to break down complex expressions into smaller, more manageable parts and work through them step-by-step. With dedication and persistence, you will become proficient in expanding and simplifying expressions.
Latest Posts
Latest Posts
-
What Did Joseph Stalin Do In World War 2
Sep 25, 2025
-
Name The Universal Force Of Attraction That Exists Between Masses
Sep 25, 2025
-
How Does Cache Size Affect The Cpu Performance
Sep 25, 2025
-
In Math What Is The Range
Sep 25, 2025
-
Difference Between B Lymphocytes And T Lymphocytes
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Expand And Simplify X 6 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.