7 6 As A Mixed Number
aseshop
Sep 08, 2025 · 6 min read
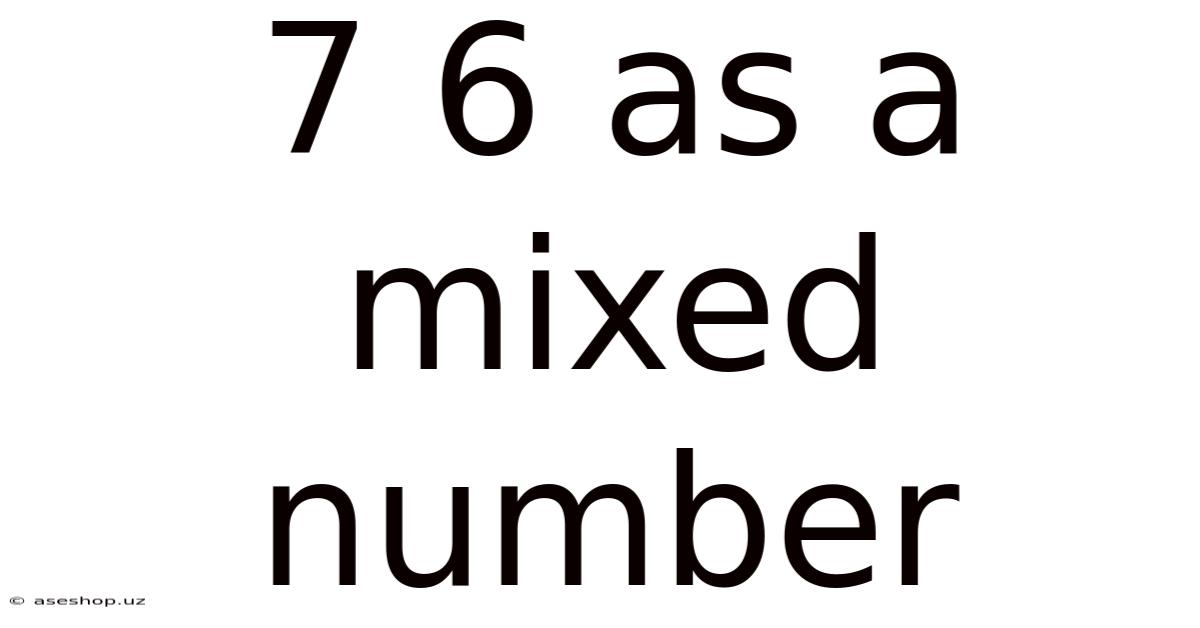
Table of Contents
Understanding 7/6 as a Mixed Number: A Comprehensive Guide
Representing fractions in different forms is a fundamental concept in mathematics. This article delves deep into understanding the improper fraction 7/6 and its equivalent mixed number representation. We'll explore the process of conversion, the underlying mathematical principles, and practical applications, ensuring a thorough understanding for learners of all levels. This guide aims to equip you with the knowledge and confidence to tackle similar fraction conversions with ease.
What is a Mixed Number?
Before we dive into converting 7/6, let's clarify the definition of a mixed number. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number), for example, 1/2, 2/5, or 3/4. Mixed numbers are a convenient way to represent quantities that are greater than one but not a whole number. For example, 2 1/3 represents two whole units and one-third of another unit.
Converting an Improper Fraction to a Mixed Number
An improper fraction is a fraction where the numerator is greater than or equal to the denominator, such as 7/6, 9/4, or 11/5. Converting an improper fraction to a mixed number involves dividing the numerator by the denominator.
Here's the step-by-step process for converting 7/6:
-
Divide the numerator by the denominator: Divide 7 by 6. 7 ÷ 6 = 1 with a remainder of 1.
-
The quotient becomes the whole number part: The quotient, 1, becomes the whole number part of the mixed number.
-
The remainder becomes the numerator of the fraction part: The remainder, 1, becomes the numerator of the fraction.
-
The denominator remains the same: The denominator remains 6.
Therefore, 7/6 as a mixed number is 1 1/6.
Visual Representation of 7/6
Imagine you have seven equal slices of a pizza. A whole pizza has six slices. You can clearly see that you have one whole pizza (six slices) and one slice remaining. This remaining slice represents 1/6 of a pizza. Thus, visually, seven slices out of six (7/6) represents 1 whole pizza and 1/6 of another pizza, confirming our calculation of 1 1/6.
The Mathematical Principle Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the principle of partitioning or dividing a quantity into equal parts. When we divide the numerator (7) by the denominator (6), we are essentially finding out how many times the denominator (6) 'fits' into the numerator (7). The quotient (1) represents the number of whole times the denominator fits, and the remainder (1) represents the remaining part that is less than the denominator, which is expressed as a fraction.
Working with Mixed Numbers: Addition and Subtraction
Mixed numbers are frequently used in everyday life, especially in situations involving measurements, cooking, or sharing quantities. Understanding how to perform basic arithmetic operations with mixed numbers is crucial.
Addition:
To add mixed numbers, you can either convert them to improper fractions first or add the whole numbers and fractions separately. Let's add 1 1/6 + 2 1/3.
-
Method 1 (Converting to Improper Fractions):
- 1 1/6 = (1*6 + 1)/6 = 7/6
- 2 1/3 = (2*3 + 1)/3 = 7/3
- 7/6 + 7/3 = 7/6 + 14/6 = 21/6 = 3 3/6 = 3 1/2
-
Method 2 (Adding Whole Numbers and Fractions Separately):
- Add the whole numbers: 1 + 2 = 3
- Find a common denominator for the fractions: 1/6 + 1/3 = 1/6 + 2/6 = 3/6 = 1/2
- Combine the whole number and fraction: 3 + 1/2 = 3 1/2
Subtraction:
Subtraction follows a similar approach. Let's subtract 1 1/6 from 3 1/2.
-
Method 1 (Converting to Improper Fractions):
- 3 1/2 = (3*2 + 1)/2 = 7/2
- 7/2 - 7/6 = 21/6 - 7/6 = 14/6 = 7/3 = 2 1/3
-
Method 2 (Subtracting Whole Numbers and Fractions Separately):
- Subtract the whole numbers: 3 - 1 = 2
- Find a common denominator for the fractions: 1/2 - 1/6 = 3/6 - 1/6 = 2/6 = 1/3
- Combine the whole number and fraction: 2 + 1/3 = 2 1/3
Real-World Applications of Mixed Numbers
Mixed numbers are incredibly useful in various real-world scenarios:
-
Cooking and Baking: Recipes often call for amounts like 2 1/2 cups of flour or 1 1/4 teaspoons of baking powder.
-
Measurements: Measuring lengths, weights, or volumes frequently involves mixed numbers, such as 3 3/4 inches or 1 1/2 kilograms.
-
Construction and Engineering: Precise measurements are essential in construction and engineering, where mixed numbers are commonly used.
-
Time: Expressing time often utilizes mixed numbers, such as 2 1/2 hours or 1 3/4 minutes.
-
Data Analysis: In data analysis, mixed numbers can represent averages or statistical measures.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn about converting improper fractions to mixed numbers?
A1: Converting between improper fractions and mixed numbers is essential for simplifying calculations and making fractions easier to understand and visualize. It also provides a more practical representation of quantities greater than one.
Q2: Can I convert any improper fraction into a mixed number?
A2: Yes, any improper fraction can be converted into a mixed number. The process of division will always yield a whole number quotient and a remainder (unless the numerator is a multiple of the denominator, in which case the remainder would be zero).
Q3: What if I get a remainder of zero when converting an improper fraction?
A3: If you get a remainder of zero, it means the improper fraction is actually a whole number. For example, if you convert 6/3, you get a quotient of 2 and a remainder of 0. This means 6/3 is equal to 2.
Q4: Are there any shortcuts for converting improper fractions to mixed numbers?
A4: While the division method is always reliable, some people find mental math shortcuts helpful. With practice, you may be able to estimate the whole number part and then calculate the remaining fraction quickly.
Q5: Is it always necessary to simplify the fractional part of a mixed number?
A5: Yes, it's best practice to simplify the fractional part of a mixed number to its lowest terms whenever possible. This makes the mixed number easier to understand and compare with other fractions. For example, 3 3/6 should be simplified to 3 1/2.
Conclusion
Understanding how to convert an improper fraction like 7/6 to its equivalent mixed number, 1 1/6, is a crucial skill in mathematics. This conversion is grounded in the fundamental principle of division and partitioning. Through this comprehensive guide, you've learned the step-by-step process, explored visual representations, and understood the mathematical rationale behind this conversion. By mastering this concept and applying it to real-world examples, you'll gain a deeper appreciation for the versatility and practical utility of fractions in everyday life and higher mathematical applications. Remember to practice regularly to reinforce your understanding and build confidence in handling fractions effectively. This knowledge will serve as a solid foundation for more advanced mathematical concepts in the future.
Latest Posts
Latest Posts
-
Good Effects Of The Industrial Revolution
Sep 08, 2025
-
Medications To Avoid With Addisons Disease
Sep 08, 2025
-
What Is It Called When Gas Turns To Liquid
Sep 08, 2025
-
What Is The Unit For Electric Current
Sep 08, 2025
-
Primary Secondary And Tertiary Care Hospitals
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 7 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.