30 Is 60 Percent Of What
aseshop
Sep 11, 2025 · 5 min read
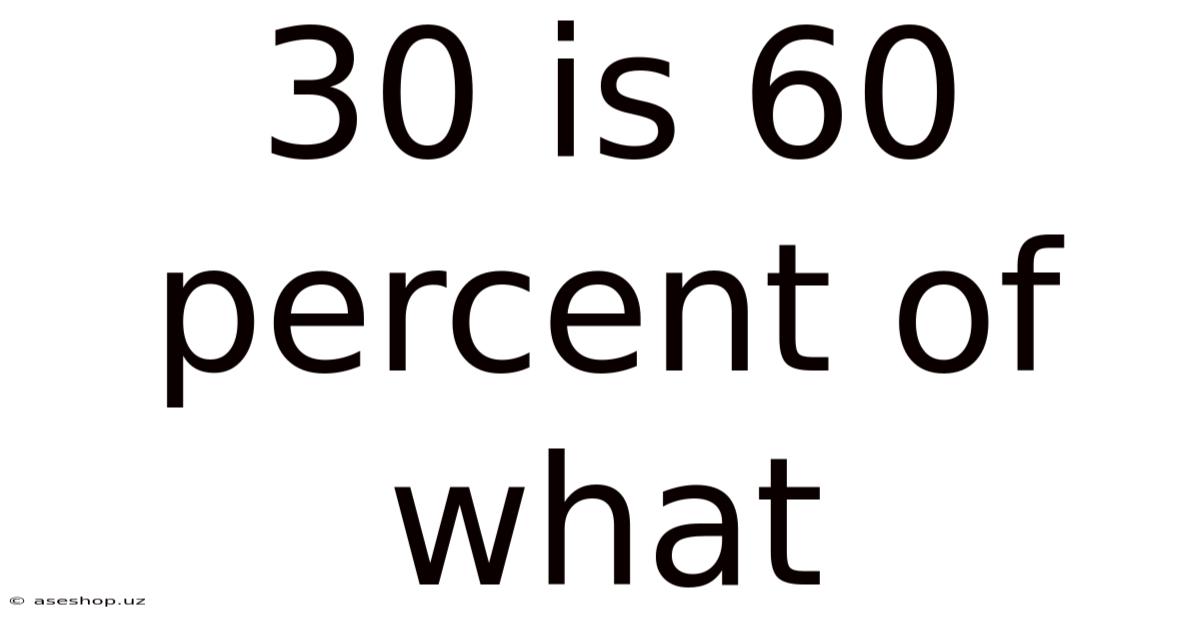
Table of Contents
30 is 60 Percent of What: A Comprehensive Guide to Percentage Calculations
Finding out what number 30 represents 60% of is a common problem encountered in various fields, from everyday budgeting to complex scientific calculations. Understanding how to solve this kind of percentage problem is crucial for anyone seeking to improve their mathematical literacy and problem-solving skills. This article will provide a step-by-step guide on how to solve this specific problem and explore the broader concept of percentage calculations, equipping you with the tools to tackle similar challenges confidently.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 60% can be written as 60/100 or 0.6 as a decimal. This representation is key to solving percentage problems.
Method 1: Using Algebra to Solve "30 is 60% of What?"
This approach utilizes algebraic equations to find the unknown value. Let's represent the unknown number as 'x'. We can translate the problem "30 is 60% of what?" into an algebraic equation:
30 = 0.6 * x
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.6:
x = 30 / 0.6
Calculating this gives us:
x = 50
Therefore, 30 is 60% of 50.
Method 2: Using Proportions to Solve "30 is 60% of What?"
Proportions offer another effective way to tackle percentage problems. A proportion sets up an equivalence between two ratios. We can set up a proportion as follows:
30/x = 60/100
This proportion states that the ratio of 30 to the unknown number (x) is equal to the ratio of 60 to 100 (60%). To solve this, we can cross-multiply:
30 * 100 = 60 * x
This simplifies to:
3000 = 60x
Now, divide both sides by 60 to isolate x:
x = 3000 / 60
x = 50
Again, we find that 30 is 60% of 50.
Method 3: Using the Percentage Formula
A more direct approach involves using the basic percentage formula:
Percentage = (Part / Whole) * 100
In our problem, we know the percentage (60%) and the part (30). We want to find the whole (x). We can rearrange the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Substituting our known values:
Whole = (30 / 60) * 100
Whole = 0.5 * 100
Whole = 50
Once again, the solution confirms that 30 is 60% of 50.
Practical Applications of Percentage Calculations
Understanding how to solve percentage problems like "30 is 60% of what?" has widespread applications in various real-world scenarios:
-
Finance: Calculating discounts, interest rates, profit margins, and tax amounts. For example, if a store offers a 60% discount on an item, and the discount amount is $30, you can use this method to determine the original price.
-
Science: Determining experimental yields, analyzing data, and expressing results as percentages. Many scientific experiments involve comparing results to a theoretical maximum, often expressed as a percentage.
-
Business: Analyzing market share, calculating sales growth, and determining return on investment (ROI). Understanding percentages helps businesses track their performance and make informed decisions.
-
Everyday Life: Calculating tips, splitting bills, and understanding sale prices. These everyday calculations make percentage proficiency a valuable life skill.
Expanding on Percentage Calculations: More Complex Scenarios
While "30 is 60% of what?" provides a basic example, percentage problems can become more complex. Here are some variations:
-
Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For instance, what percentage is 15 of 75?
-
Finding the Part: If you know the percentage and the whole, you can find the part. For example, what is 25% of 80?
-
Problems involving multiple percentages: Situations may involve calculating consecutive percentage changes, such as a 10% increase followed by a 5% decrease.
Step-by-Step Guide to Solving General Percentage Problems
To solve any percentage problem, follow these steps:
-
Identify the known values: Determine which values are given (percentage, part, whole).
-
Identify the unknown value: Determine what needs to be calculated (percentage, part, whole).
-
Choose the appropriate formula: Select the formula that best suits the known and unknown values.
-
Substitute the known values: Replace the variables in the chosen formula with the known values.
-
Solve the equation: Use algebraic manipulations to isolate and calculate the unknown value.
-
Check your answer: Verify your answer using a different method or by re-checking your calculations.
Frequently Asked Questions (FAQs)
Q: What if the percentage is greater than 100%?
A: Percentages greater than 100% indicate that the "part" is larger than the "whole." This often occurs when comparing changes or growth over time. The same principles of percentage calculations apply, but the result will be a number larger than the "whole."
Q: How can I calculate percentage increase or decrease?
A: To calculate percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For percentage decrease, follow the same process but subtract the new value from the original value.
Q: Are there any online calculators or tools to help with percentage calculations?
A: Yes, numerous online calculators are available that can perform various percentage calculations, including finding the whole when given the part and percentage.
Conclusion
Solving "30 is 60% of what?" involves understanding the fundamental principles of percentage calculations. Whether you use algebra, proportions, or the percentage formula, the answer remains the same: 50. Mastering these methods not only helps you solve this specific problem but equips you with the skills to tackle various percentage calculations in various contexts. By understanding the underlying concepts and practicing these methods, you'll build confidence in your mathematical abilities and apply this knowledge to solve real-world problems effectively. Remember to always break down complex problems into smaller, manageable steps, and double-check your work to ensure accuracy. With practice, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
What Is The Sanctity Of Life
Sep 11, 2025
-
Is A Plant Cell Prokaryotic Or Eukaryotic
Sep 11, 2025
-
Four Links In The Chain Of Survival
Sep 11, 2025
-
What Is The Game Pin For Kahoot
Sep 11, 2025
-
Wishing U Were Somehow Here Again Lyrics
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 30 Is 60 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.