17 Out Of 25 As A Percent
aseshop
Sep 17, 2025 · 5 min read
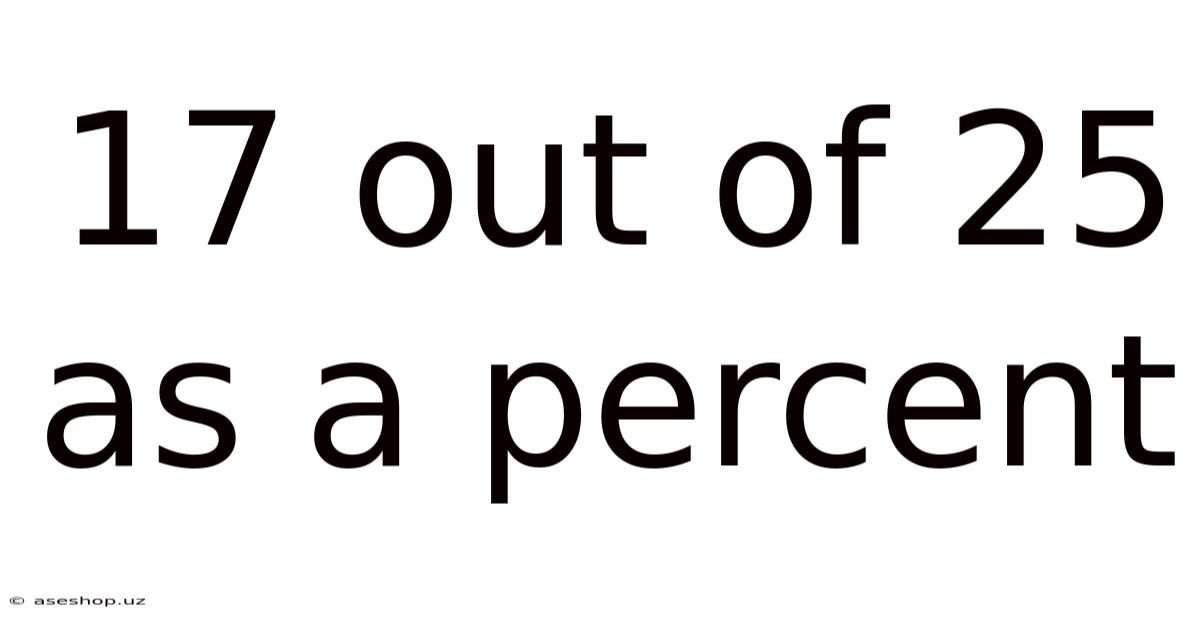
Table of Contents
17 out of 25 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into how to calculate "17 out of 25 as a percent," providing not only the answer but also a deeper understanding of the underlying principles and various methods for solving similar problems. This will cover various approaches, including the standard formula, using proportions, and even exploring the concept within the context of real-world applications.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Therefore, to express a fraction as a percentage, we determine what part of 100 that fraction represents. This process is crucial in numerous fields, including finance, science, and everyday decision-making.
Method 1: The Standard Percentage Formula
The most straightforward method for calculating "17 out of 25 as a percent" involves using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 17 (the number we're considering as a portion of the whole)
- Whole: 25 (the total number)
Applying the formula:
(17 / 25) x 100% = 68%
Therefore, 17 out of 25 is equal to 68%.
Method 2: Using Proportions
Another approach involves setting up a proportion. We know that a percentage is a fraction out of 100. We can set up a proportion to solve for the unknown percentage (x):
17/25 = x/100
To solve for x, we can cross-multiply:
17 * 100 = 25 * x
1700 = 25x
x = 1700 / 25
x = 68
Therefore, x = 68%. This method demonstrates the equivalence between fractions and percentages.
Method 3: Decimal Conversion
We can also approach this by first converting the fraction to a decimal and then converting the decimal to a percentage.
17 / 25 = 0.68
To convert a decimal to a percentage, we simply multiply by 100%:
0.68 x 100% = 68%
This method highlights the relationship between decimals and percentages, reinforcing the understanding of their interconnectedness.
Expanding the Concept: Variations and Applications
The calculation of "17 out of 25 as a percent" serves as a foundation for understanding more complex percentage problems. Let's explore some variations and practical applications:
-
Calculating Percentage Increase/Decrease: Imagine a scenario where a price increases from 25 to 42. To calculate the percentage increase, we first find the difference (42 - 25 = 17), then divide by the original value (17/25) and multiply by 100%. This reveals a 68% increase. Similarly, we can calculate percentage decreases.
-
Finding the Whole when given a percentage and a part: If we know that 68% of a quantity is 17, we can set up an equation to find the whole. Let's represent the whole as "x":
0.68x = 17
x = 17 / 0.68
x = 25
This shows that if 68% represents 17, the total amount (or whole) is 25.
-
Real-world examples: This skill is vital in many everyday situations:
- Grade Calculation: If a student answers 17 out of 25 questions correctly on a test, their score is 68%.
- Sales and Discounts: A store offering a 68% discount on an item priced at $25 will reduce the price by $17 ($25 x 0.68 = $17).
- Financial Analysis: Investors use percentages to track returns on investments, growth rates, and other key financial metrics. Understanding percentage changes is crucial for evaluating financial performance.
- Statistical Analysis: Percentages are fundamental to describing data sets. For example, in surveys, percentages are used to represent the proportion of respondents who selected particular options.
Frequently Asked Questions (FAQ)
-
What if the numbers are larger? The methods described above apply regardless of the size of the numbers. You can use a calculator to simplify the calculations for larger numbers.
-
How do I round percentages? Depending on the context, you may need to round percentages to a certain number of decimal places. Generally, rounding to one or two decimal places is sufficient for most practical purposes. For example, 68.23% rounded to the nearest whole number would be 68%.
-
What if I need to calculate a percentage of a percentage? To calculate a percentage of a percentage, you simply multiply the two percentages together. For instance, 50% of 68% is (0.50)(0.68) = 0.34 or 34%.
-
What are some common percentage mistakes to avoid? One common mistake is forgetting to divide by the whole before multiplying by 100%. Always ensure you're performing the division correctly before calculating the percentage. Also, be careful with rounding errors, especially when dealing with more complex calculations.
Beyond the Basics: Advanced Concepts
While calculating 17 out of 25 as a percent is a straightforward calculation, mastering percentages extends beyond basic computations. Understanding compound interest, percentage points, and applying percentage calculations in various statistical analyses are advanced concepts that build upon this fundamental skill. For example, understanding compound interest allows you to predict the future value of investments or loans, incorporating the effect of interest earned on both the principal and accumulated interest. Percentage points, on the other hand, represent the arithmetic difference between two percentages, not the percentage difference between them. For example, an increase from 10% to 20% represents a 10-percentage-point increase but a 100% percentage increase.
Conclusion
Calculating "17 out of 25 as a percent" is a simple yet crucial skill. Understanding the underlying principles, the different methods for calculating percentages, and their wide range of applications provides a solid foundation for tackling more complex mathematical problems and navigating real-world situations. Whether it's assessing test scores, understanding discounts, or analyzing financial data, proficiency in percentage calculations is an invaluable asset in various aspects of life. Remember to practice regularly and familiarize yourself with different approaches to build confidence and mastery of this fundamental skill. By understanding the various approaches and their applications, you can confidently tackle any percentage-related problem, transforming seemingly daunting calculations into manageable and understandable tasks.
Latest Posts
Latest Posts
-
Who Was President During Vietnam War
Sep 17, 2025
-
Mouth Of A Volcano Crossword Clue
Sep 17, 2025
-
What Was The Reason For The Cold War
Sep 17, 2025
-
How Do Prokaryotic And Eukaryotic Cells Differ
Sep 17, 2025
-
Labelling The Parts Of A Plant
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 17 Out Of 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.