1 2 X 1 X 2
aseshop
Sep 05, 2025 · 6 min read
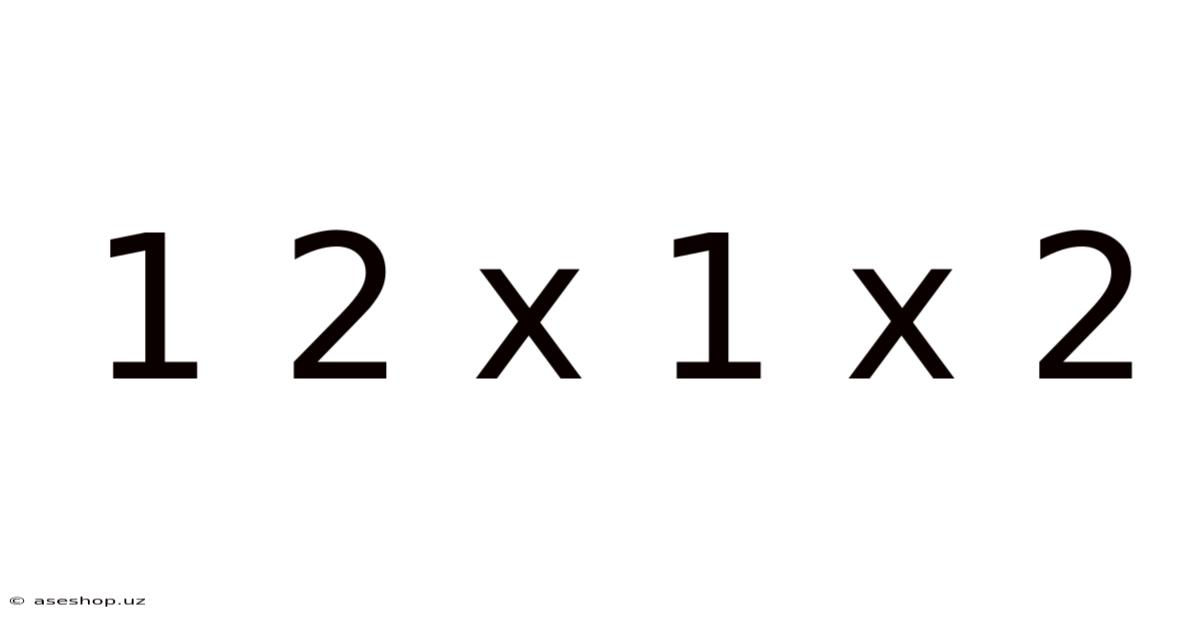
Table of Contents
Decoding 1 x 2 x 1 x 2: A Deep Dive into Mathematical Operations and Their Applications
This article explores the seemingly simple mathematical expression "1 x 2 x 1 x 2," delving beyond the immediate answer to uncover its underlying principles, practical applications, and connections to broader mathematical concepts. We will examine the fundamental operations involved, explore the order of operations, and discuss how this simple equation can serve as a building block for understanding more complex calculations. This seemingly basic expression offers a gateway to grasping crucial mathematical foundations, applicable in various fields.
Understanding the Fundamentals: Multiplication and Order of Operations
At its core, "1 x 2 x 1 x 2" involves the fundamental arithmetic operation of multiplication. Multiplication is essentially repeated addition. For example, 1 x 2 is the same as adding 1 to itself two times (1 + 1 = 2). In our expression, we have multiple multiplications performed sequentially. The order in which we perform these operations is crucial and is governed by the rules of order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
Since our expression contains only multiplication, we can perform the operations from left to right:
- 1 x 2 = 2
- 2 x 1 = 2
- 2 x 2 = 4
Therefore, the solution to 1 x 2 x 1 x 2 is 4. This simple calculation highlights the commutative and associative properties of multiplication.
The Commutative Property: Order Doesn't Matter
The commutative property of multiplication states that the order of the numbers being multiplied does not affect the final result. This means that 1 x 2 is the same as 2 x 1. We can rearrange the numbers in our expression without changing the outcome:
- 1 x 2 x 1 x 2 = 4
- 2 x 1 x 2 x 1 = 4
- 1 x 1 x 2 x 2 = 4
- and so on...
This property is fundamental in simplifying complex mathematical expressions and is crucial in various applications, such as matrix algebra and linear transformations.
The Associative Property: Grouping Doesn't Matter
The associative property of multiplication states that the grouping of numbers in a multiplication problem does not affect the result. We can group the numbers differently using parentheses without changing the final answer:
- (1 x 2) x (1 x 2) = 2 x 2 = 4
- 1 x (2 x 1) x 2 = 1 x 2 x 2 = 4
- 1 x 2 x (1 x 2) = 2 x 2 = 4
This property is particularly useful when dealing with larger expressions, allowing for efficient simplification. It is a cornerstone of algebraic manipulation and is widely used in solving equations and simplifying complex formulas.
Beyond the Basic Calculation: Expanding the Scope
While the calculation itself is straightforward, understanding the underlying principles opens doors to more complex mathematical ideas. Let's explore some of them:
Expanding to More Complex Multiplications:
We can easily expand this concept to include more numbers. For example: 1 x 2 x 1 x 2 x 3 would be solved as follows:
- 1 x 2 = 2
- 2 x 1 = 2
- 2 x 2 = 4
- 4 x 3 = 12
The result would be 12. This illustrates how the fundamental principles of multiplication and order of operations extend to more complex scenarios.
Introducing Variables:
Instead of using only numbers, we can introduce variables. For example, consider the expression: a x 2 x b x 2, where a and b represent any numbers. This expression can be simplified using the commutative and associative properties:
a x 2 x b x 2 = 4a b
This shows how the same fundamental principles apply even when dealing with algebraic expressions. This is essential for solving equations and working with formulas in algebra and calculus.
Applications in Real-World Scenarios:
The principles embedded in this simple calculation have far-reaching applications in various fields:
-
Area Calculation: If you have a rectangular area with dimensions 1 unit by 2 units, and you have two such rectangles, then finding the total area involves the calculation 1 x 2 x 1 x 2, resulting in 4 square units.
-
Volume Calculation: Similarly, you might be calculating the volume of a rectangular prism. The calculation 1 x 2 x 1 x 2 might represent a portion of this calculation.
-
Combinatorics and Probability: The concept of multiplication is central to combinatorics and probability. For instance, if you have two choices for a shirt (1 and 2) and two choices for pants (1 and 2), the total number of possible outfits is given by 1 x 2 x 1 x 2 = 4.
-
Computer Programming: In programming, multiplication is a fundamental operation used in loops, array manipulation, and various algorithms.
-
Engineering and Physics: Many engineering and physics problems involve multiplications to model and solve complex systems.
Frequently Asked Questions (FAQ)
Q: What if there were parentheses in the expression?
A: The presence of parentheses would alter the order of operations. For example, (1 x 2) x (1 x 2) is evaluated differently, as the operations within the parentheses are performed first. This highlights the importance of understanding the order of operations and how parentheses modify it.
Q: Can I use a calculator for this calculation?
A: Absolutely! Even though the calculation is simple, using a calculator can be beneficial for checking your work or for more complex calculations based on this principle.
Q: What if the numbers were different?
A: The same principles still apply. The order of operations, the commutative property, and the associative property would still hold true, regardless of the specific numbers used in the expression.
Q: How does this relate to more advanced mathematics?
A: This simple equation provides a foundational understanding of mathematical operations that are crucial for more advanced concepts. It forms the basis for understanding algebra, calculus, linear algebra, and other mathematical fields. The properties explored here are fundamental to many advanced mathematical theorems and proofs.
Conclusion: The Significance of Simplicity
The seemingly simple expression "1 x 2 x 1 x 2" offers a surprisingly rich learning opportunity. Beyond its straightforward answer of 4, it serves as a powerful tool for understanding fundamental mathematical concepts such as multiplication, order of operations, commutative property, and associative property. These principles are not merely abstract rules but are the building blocks for more complex mathematical calculations and real-world applications across diverse fields. By mastering the basics, we equip ourselves with the foundation to tackle more challenging mathematical problems and appreciate the elegance and power of mathematical reasoning. This simple expression underscores that even the most basic mathematical concepts can lead to deep and significant insights.
Latest Posts
Latest Posts
-
How To Calculate Rf Value Chromatography
Sep 05, 2025
-
How Many Calories In 1 Gram Of Carbs
Sep 05, 2025
-
Quote Neither A Borrower Nor A Lender Be
Sep 05, 2025
-
Why Did Wrigley Kill His Aunt
Sep 05, 2025
-
Difference Between A Compound And Mixture
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 1 2 X 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.